Meeting NYS Math Fluency Standards: Strategies for K–2 Teachers

What is Computational Fluency?

Many people think of computational fluency as simply being able to recall math facts quickly. But true fluency is much more than speed - it involves a deep understanding of numbers and strategies.

Computational fluency is demonstrated through four key components:

• Accuracy: Producing mathematically precise answers.
• Efficiency: Solving problems quickly and with ease.
• Appropriate Strategy Use: Selecting and applying strategies that make sense for the problem.
• Flexibility: Thinking about problems in multiple ways and adjusting strategies when needed.

What Do the NYS Standards Say?

The New York State Standards outline specific fluency expectations for Kindergarten - 2nd grade students:

• NYS-K.OA.5 Fluently add and subtract within 5.
• NYS-1.OA.6b Fluently add and subtract within 10.
  
• NYS-2.OA.2a Fluently add and subtract within 20 using mental strategies.
  

By the end of second grade, students are expected to "know from memory all sums within 20 of two one-digit numbers." (NYS-2.OA2b). But what does it mean to "know from memory?" There’s an important difference between memorizing facts and knowing them from memory:

• Memorizing relies on rote repetition - think flashcards and timed tests.
  

• Knowing from memory develops through strategy use and repeated meaningful practice.
  

When students use strategies over and over, they become automatic. The NYS Standards recognize that having a bank of strategies and being able to apply them to new situations, rather than simply recalling facts, is more powerful than memorization in the long term and promotes higher-order thinking.

Effective Strategies for Building Fact Fluency

Some students naturally discover efficient strategies on their own. Others benefit from explicit instruction and structured opportunities to build mental reasoning strategies. Research shows that one of the most effective ways for students to master basic addition facts (0 + 0 through 9 + 9) is to group them into clusters. This helps students build connections between problems and allows them to use known facts to solve new ones, which is more efficient than rote memorization of all facts individually.

Three key clusters cover all 100 basic addition facts: Count On, Use Doubles and Make a Ten.

1. Count On
This cluster includes facts with an addend of 0, 1, 2, or 3. The light blue shading in the addition table below shows the 64 addition Count On facts.
Example: 5+3 (and its turnaround fact 3+5) can be solved by starting at the larger number (5) and counting on the smaller number (3): 5…6, 7, 8 - it's 8!

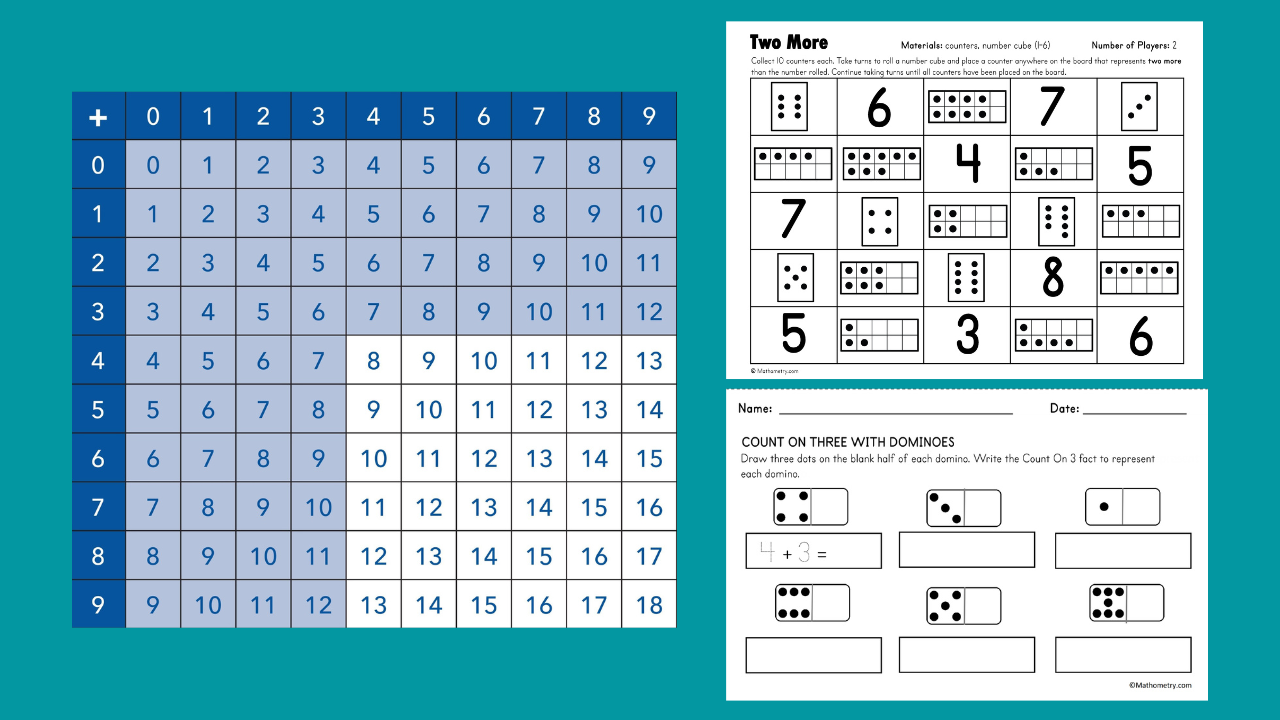
2. Use Doubles
This cluster includes doubles facts (e.g., 3+3, 6+6) and near doubles facts (4+5, 8+7). The light blue shading in the addition table below shows the 44 Use Doubles facts (doubles, doubles plus 1, doubles plus 2, doubles minus 1, doubles minus 2).
Example: 6+7 can be solved using the Doubles fact 6+6 and adding one more: 6 + 6 + 1 = 13; 9 + 8 can be solved using the Doubles fact 9+9 and subtracting one: 9 + 9 - 1 = 17.

3. Make a Ten (sometimes referred to as Bridge to Ten)
This cluster includes facts where one addend is 7, 8, or 9. The light blue shading in the addition table below shows the 33 Make a Ten facts.
Example: 8+6 can be solved by partitioning 6 into 2 and 4 and adding the 2 to 8 to make a ten: 8+2=10; 10+4=14.

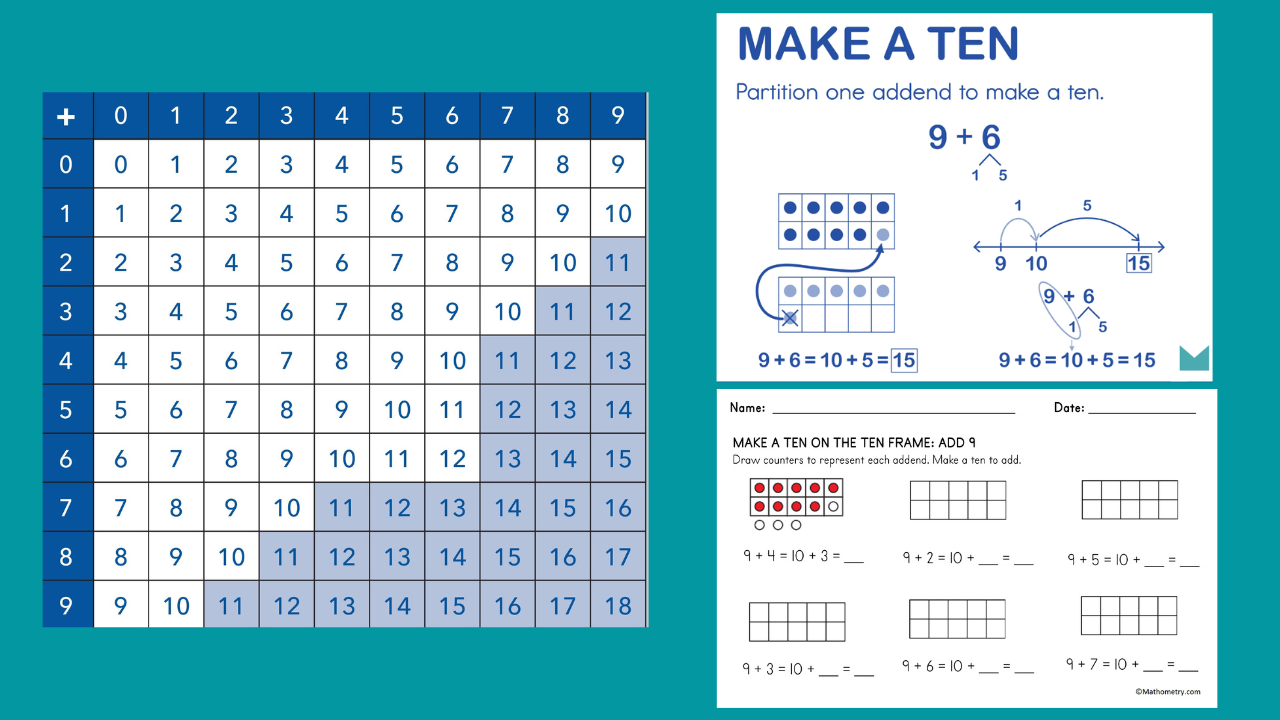 Some facts can be solved with more than one strategy. For example, 8+6 can be solved using the Doubles fact 8+8 and subtracting two: 8 + 8 - 2 = 14  or by using the Make a Ten strategy (8 + 2 + 4 = 14). Encouraging students to explore multiple strategies helps build flexibility and confidence.

Stages of Teaching and Learning 

As we teach these strategies, it’s important to consider four stages of learning:

1. Build Prerequisite Skills
 Before introducing a strategy, make sure students have the foundational skills to support it. For example:

• A strong understanding of cardinality is essential for using the Count On strategy.

• Fluency with Doubles facts is needed to use the Near Doubles strategy.

• Fluency in adding ten to a one-digit number is necessary to use the Make a Ten strategy effectively.

2. Introduce the Strategy
Use concrete materials (e.g., counters, ten frames) and pictorial representations to build a strong conceptual understanding before moving to abstract representations.

3. Provide Ample Practice
Offer repeated, meaningful practice through fluency centers, games, math journal tasks, and number talks so students can internalize the strategy. Time-limited practice should be introduced only after students demonstrate accuracy with a strategy.

4. Extend and Apply
Students who are ready can apply these strategies to larger numbers. 
Example: 28+15 can be solved mentally using Make a Ten by partitioning the smaller addend to make a multiple of ten (28+15 = 30+13 = 43). Similarly, 398 + 47 can be solved by partitioning 47 into 2 and 45: 398 + 47 = 400 + 45 = 445.

Developing computational fluency is about far more than speed. It’s about understanding numbers, choosing efficient strategies, and building flexibility. With intentional instruction, structured practice, and opportunities to think strategically, students can develop the kind of fluency that supports them throughout their mathematical journey.

Looking for resources to build addition and subtraction fact fluency? Download these sample pages, then head to the All Access Math Hub for immediate access to lots more ideas and downloads!